¿Qué sería de nuestras vidas si no existieran los números?
El despertador que no suena, el dinero que no existe, nada se puede medir ni contar, no hace falta ir a trabajar porque no ganarás nada. No habría celulares, ni computadoras, ni televisión, ni fútbol.
Nada.
Las matemáticas no lo son todo, pero están presentes en todos los ámbitos de nuestra vida.
Un nuevo año comienza, y siempre es divertido analizar el número que nos gobernará a todos. Aunque siempre nos cuesta cambiar de año, sobre todo en las carpetas de clase (el 2015 tardará en desaparecer).
Entramos en un año bisiesto y olímpico. De esos tipos “raros” que pasan cada cuatro años y de los que siempre (al menos yo) nos acordamos. Recuerdos deportivos que dejan pinceladas de nuestra juventud. Me hago más mayor aunque siga siendo un niño (por suerte).
Febrero será más largo.
Y muy contentos se ponen los que celebran su cumpleaños cada cuatro años. Estos “afortunados”, siempre jóvenes, incluso han creado un club mundial de los bisiestos y celebran actividades el 29 de febrero.
¿Cómo es el número 2016, que sorpresas nos esconde?
En este artículo solo quiero hacerte partícipe de un simple pasatiempo. Veremos cómo es este precioso número de cuatro cifras y te darás cuenta de las curiosidades matemáticas que contiene en su interior.
En principio parece un número normalito y sencillo. Muy redondo, par y poco más, pero investigando un poco sobre las matemáticas del 2016 descubrimos esto …
Es un número triangular
¿Cómo? ¿Dónde se esconde el triángulo?
Los números triangulares son números figurados, es decir, aquellos números que pueden representarse mediante figuras geométricas “regulares”
Los primeros números triangulares son estos: 1, 3, 6, 10, 15, 21, 28, 36.
Un número triangular se puede obtener sumando números naturales consecutivos (10=1+2+3+4)
Asimismo 2016 es un número triangular porque 1+2+3+4+ …..+ 63 = 2016
También es un número hexagonal !! Ninguno de nosotros vivió en el último año hexagonal (1891), ni tampoco viviremos el siguiente (2145)
¿Cuántos apretones de manos habrá en un congreso o reunión de 64 personas?
Relacionado con lo anterior, y en el caso que todos lo hagan cordialmente, habrán 2016 saludos.
En este caso (como en muchos otros) haciendo dibujos y siguiendo el patrón matemático que se repite, encontraremos la solución.
Representaremos cada persona con un punto, y el saludo (apretón de manos) con un segmento. Pronto observamos que el total de saludos para 4 o más personas es la suma de los lados del polígono más las diagonales de dicho polígono. Y vemos que algo se repite …


Otra vez aquí, aparecen los números triangulares …
Efectivamente, has vuelto a adivinarlo! … 2016
Hay que recordar un poco de combinatoria para obtener este número. La manera de combinar 64 casillas en grupos de 2 es esta:
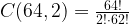
Algunas formas sencillas y atractivas de expresar el nuevo año
Con tres números sencillos y fáciles de recordar

Mediante números factoriales

Como resta de cuadrados

Como suma de cubos

Con el número de la bestia en su interior, o si lo prefieres con seises.
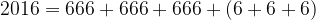
Y el más fácil de recordar …

Breve resumen de las matemáticas del 2016
Factorización: 2^5 · 3^2 · 7
Divisores: 1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 16, 18, 21, 24, 28, 32, 36, 42, 48, 56, 63, 72, 84, 96, 112, 126, 144, 168, 224,252, 288, 336, 504, 672, 1008, 2016
Número de divisores: 36
Primo anterior: 2011 Siguiente número primo: 2017
2016 en sistema binario: 11111100000
Muchas de estas expresiones las he visto en twitter, son de Antonio Roldán @Connumeros. Te recomiendo que te pases por su web hojamat.es
Si no te gusta este número por ser muy redondo, el próximo será tu año, porque 2017 es un número primo y dará mucho juego. Pero eso ya te lo contaré dentro de un año …
Te deseo un feliz y próspero año 2016 , repleto de salud y matemáticas!!
Es un número triangular
¿Cómo? ¿Dónde se esconde el triángulo?
Los números triangulares son números figurados, es decir, aquellos números que pueden representarse mediante figuras geométricas “regulares”
Los primeros números triangulares son estos: 1, 3, 6, 10, 15, 21, 28, 36.
Un número triangular se puede obtener sumando números naturales consecutivos (10=1+2+3+4)
Asimismo 2016 es un número triangular porque 1+2+3+4+ …..+ 63 = 2016
También es un número hexagonal !! Ninguno de nosotros vivió en el último año hexagonal (1891), ni tampoco viviremos el siguiente (2145)
¿Cuántos apretones de manos habrá en un congreso o reunión de 64 personas?
Relacionado con lo anterior, y en el caso que todos lo hagan cordialmente, habrán 2016 saludos.
En este caso (como en muchos otros) haciendo dibujos y siguiendo el patrón matemático que se repite, encontraremos la solución.
Representaremos cada persona con un punto, y el saludo (apretón de manos) con un segmento. Pronto observamos que el total de saludos para 4 o más personas es la suma de los lados del polígono más las diagonales de dicho polígono. Y vemos que algo se repite …


Otra vez aquí, aparecen los números triangulares …
Combinatoria y ajedrez
¿Cuál es el número de pares de casillas diferentes que se pueden elegir en un tablero de ajedrez?Efectivamente, has vuelto a adivinarlo! … 2016
Hay que recordar un poco de combinatoria para obtener este número. La manera de combinar 64 casillas en grupos de 2 es esta:
Algunas formas sencillas y atractivas de expresar el nuevo año
Con tres números sencillos y fáciles de recordar
Mediante números factoriales
Como resta de cuadrados
Como suma de cubos
Con el número de la bestia en su interior, o si lo prefieres con seises.
Y el más fácil de recordar …
Breve resumen de las matemáticas del 2016
Factorización: 2^5 · 3^2 · 7
Divisores: 1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 16, 18, 21, 24, 28, 32, 36, 42, 48, 56, 63, 72, 84, 96, 112, 126, 144, 168, 224,252, 288, 336, 504, 672, 1008, 2016
Número de divisores: 36
Primo anterior: 2011 Siguiente número primo: 2017
2016 en sistema binario: 11111100000
Muchas de estas expresiones las he visto en twitter, son de Antonio Roldán @Connumeros. Te recomiendo que te pases por su web hojamat.es
Si no te gusta este número por ser muy redondo, el próximo será tu año, porque 2017 es un número primo y dará mucho juego. Pero eso ya te lo contaré dentro de un año …
Te deseo un feliz y próspero año 2016 , repleto de salud y matemáticas!!














































