Día mundial de la alimentación

Ayer 16/10 se celebró el Día mundial de la alimentación, su finalidad es concientizar a los pueblos del mundo sobre el problema alimentario mundial y fortalecer la solidaridad en la lucha contra el hambre, la desnutrición y la pobreza. .

ⒹⒶⓉⓄ

En Argentina se desperdician por año 16 millones de toneladas y todavía hay gente que no tiene para comer.

31 de Mayo - Día del Matemático

La matemática te recuerda la forma invisible del alma; da luz a sus propios descubrimientos; despierta la mente y purifica el intelecto; ilumina nuestras ideas intrínsecas; elimina el olvido y la ignorancia que nace con nosotros.

Matemáticas

Las matemáticas son una​ materia inmensa y nadie puede conocerlas en su totalidad. Lo que si podemos hacer es explorarlas y hallar nuestro camino individual.

Las matemáticas son al mismo tiempo antiguas y modernas y se han desarrollado a partir de amplias influencias culturales y políticas. De India y Arabia procede nuestro sistema de numeración moderno, pero este a sido templado a lo largo de la historia con elementos de diversas procedencias. La "base 60" de los babilonios del segundo o tercer milenio a.C. aparece en nuestra propia cultura: tenemos 60 segundos en un minuto o 60 minutos en una hora; un ángulo recto sigue siendo de 90 grados y no de 100 grados, como el que adoptó la  Francia revolucionaria, que dio un primer paso hacia la decimalización.

Los triunfos tecnológicos de la edad moderna dependen de las​ matemáticas. Naturalmente, las matemáticas escolares son algo distinto, algo que a menudo se enseña con vistas a los exámenes. La presión temporal del colegio tampoco ayuda, ya que las matemáticas son una materia en la que no tiene sentido ir deprisa. La gente necesita tiempo para poder asimilar las ideas. Algunos de los más grandes matemáticos han sido exasperante lentos en sus esfuerzos por comprender los conceptos profundidad día de su materia.

Estamos en un momento emocionante para las matemáticas. Algunos de sus problemas más importantes se han resuelto en los últimos tiempos. Los avances de la informática moderna han ayudado a algunos, pero han resultado inútiles frente a otros. El problema de los cuatro colores se resolvió con la ayuda de una computadora, pero la hipótesis de Riemann, sigue sin resolverse: aún no se ha conseguido, ni por computadora ni por ningún otro medio.

Las matemáticas son para todo el mundo. La popularidad del sudoku es la prueba de que la gente puede hacer matemáticas (sin saberlo) y también disfrutar de ello. En las matemáticas, como en el arte o la música, ha habido genios, pero no solo ellos han hecho la historia.

Federico G. Gutierrez
- Profesor de Matemática -

Los recuerdos viajan por el cerebro mientras dormimos

Desde hace años, la ciencia afirma que dormir es crucial para el aprendizaje y la formación de memoria a largo plazo. Pero exactamente cómo se forma dicha memoria es algo que aún no se comprende del todo y se ha convertido en una cuestión central de la investigación en neurociencias.

Ahora un grupo de neurocientíficos de la Universidad de California, Riverside aseguran que podrían tener una respuesta a esta pregunta: según el estudio, publicado en Journal of Neuroscience, el sueño profundo (también llamado sueño de onda lenta) puede ser el responsable de la transformación de los recuerdos recientes en memorias de largo plazo.

Durante el sueño, el cerebro humano y animal se aísla de gran parte de la información sensorial, lo que no quiere decir que esté inactivo, todo lo contrario. Se puede observar gran actividad en el hipocampo (región vinculada a la memoria) y en el córtex, alternando períodos de estados activos e inactivos de las neuronas corticales durante el sueño profundo.

Utilizando un modelo computacional, los investigadores de la Universidad de California Riverside han señalado un vínculo entre la actividad eléctrica en el cerebro durante el sueño profundo y las conexiones sinápticas entre las neuronas. De acuerdo con este modelo, la actividad del hipocampo modifica las oscilaciones en el córtex produciendo cambios en las sinapsis de esta región, algo determinante ya que los cambios en las conexiones entre neuronas están asociados al aprendizaje y a la consolidación de la memoria en el cerebro.

“Las oscilaciones se mantuvieron estables aún sin estar infuidas por el hipocampo – explica Yina Wei, una de las responsables del estudio – . Esto nos lleva a deducir que durante el sueño profundo, los recuerdos se consolidan en el córtex y se vuelven independientes del hipocampo”.

Analema Solar

El analema representa la figura trazada en el cielo por las diferentes posiciones del Sol levantadas a una misma hora del tiempo universal y desde el mismo lugar en el curso de un año calendario.
La forma del analema depende de la hora. A eso de las doce local, la forma del ocho es casi vertical con relación al meridiano.
A una otra hora del día el ocho son inclinados a la izquierda, por la mañana o a la derecha, la tarde. Sobre Tierra, el analema tiene una forma de "8", pero sobre Marte tiene la forma de una " gota de agua ".
Cada día a la misma hora, una foto del cielo con la posición del Sol visible, mostraría que el Sol no se quedaba siempre a la misma posición.
La figura en forma de "8" que el Sol dibuja cada día en el cielo en el curso de un año, se llama un analema. Estas fluctuaciones son debidas al hecho de que el movimiento de la Tierra alrededor del Sol no es completamente circular ni completamente uniforme.
El desplazamiento aparente del Sol es causado a la vez por el desplazamiento de la Tierra alrededor del Sol y por la inclinación del eje de rotación de nuestro planeta. El Sol está en la cumbre del analema al solsticio de verano, está abajo el analema al solsticio de invierno. El invierno, el Sol es muy próximo del horizonte y en verano es muy alto en el cielo.
Según la latitud de la que están hechos los analemas, tienen pequeñas diferencias, como los tomados en diferentes momentos cada día. Analema del Sol está más cerca de la ecuación del tiempo. 

Analema solar, Atenas, 20o3

Analema solar, Buenos Aires, 2013-2014

 

14/4/2003: Final de la secuenciacion del genoma humano

El Proyecto Genoma Humano (1990-2003) fue un proyecto de investigación biomédica para determinar la secuencia de pares de bases químicas que componen el ADN e identificar el genoma humano.

Representación gráfica del cariotipo humano normal

El 14 de abril de 2003, el National Human Genome Research Institute (NHGRI) anunció la finalización del proyecto.

Progresiones geométricas sorprendentes

Siempre he pensado que es importante enlazar la historia de las matemáticas con su enseñanza, de tal forma que los alumnos puedan ver como han ido avanzando las matemáticas según las necesidades de la humanidad. ¿Cuándo se inventaron los números?, ¿cuando surgió el cero?, ¿y las funciones?, ¿podríamos vivir sin matemáticas?

Y contar historias en el aula también motiva a los chicos. El tema de sucesiones y progresiones de 3º de secundaria suele dar mucho juego. ¡Hay que aprovecharlo!

El inventor del ajedrez

Dicen y cuentan que hace ya mucho tiempo hubo un rey absorto y maravillado con el fascinante juego del ajedrez. Tan encantado estaba que ofreció a su inventor concederle lo que pidiera.
“Sólo te pido 1 grano de trigo por la primera casilla, 2 por la segunda, 4 por la tercera, 8 por la cuarta y así sucesivamente. En cada una el doble que la anterior hasta llegar a la última, la casilla número 64.”

Al rey le pareció algo insignificante y pensó que el inventor era muy humilde. Pero estaba muy equivocado.
¿A cuántos granos de trigo asciende la deuda que el rey contrajo con el inventor del ajedrez?

La sucesión sería esta:

Se trata de una progresión geométrica cuyo primer término es 1 y su razón es 2. Por tanto, el último término, que corresponde a la última casilla es 2 elevado a 63, es decir una cantidad gigantesca; la cantidad total la tienes aquí abajo. El rey no pudo conceder su promesa, al no haber suficiente trigo en toda la tierra para satisfacer los deseos del inventor del ajedrez.

Para que te hagas una idea, con tal cantidad de volumen de trigo, se podría cubrir toda la ciudad de Nueva York llegando a una altura de 1500 metros.

Las Torres de Hanoi
Tal vez hayas visto alguna vez este juego. Se trata de una estructura de 3 varillas donde se insertan varios discos de diferentes tamaños. Inicialmente los discos se sitúan en la varilla de la izquierda colocados de mayor a menor. El juego consiste en pasar todos los discos a la varilla de la derecha, teniendo en cuenta que en cada movimiento sólo puedes pasar un disco a un lugar vacío o situarlo encima de otro disco de mayor tamaño.

Cuenta una leyenda que Dios colocó 64 discos en la varilla de la izquierda y dijo ” Cuando la humanidad concluya este juego se acabará el mundo”.
El número de movimientos de este juego está en función del número de discos (n). Y se trata de una sucesión cuyo término general es

Los primeros términos de esta sucesión son: 1, 3, 7, 15, 31, 63, …
¿Cuanto tiempo se tardaría en completar el juego utilizando 64 discos? Nos harían falta movimientos. Haciendo la suposición de 1 segundo por movimiento, tardaríamos 585 mil millones de años (más de cuarenta veces la edad estimada del universo).

Doblando papel. Una progresión asombrosa
Posiblemente te hayas preguntado alguna vez cuántas veces puedes doblar una hoja de papel. Y hayas jugado a ver quien es capaz de doblar más veces un folio.
Pero, imagínate ahora que pudieras doblar las veces que quisieras una hoja de papel de 0,14 mm. de grosor. Cada vez que haces un pliegue por la mitad se duplica su grosor, ¿verdad?, El grosor del papel tras un doblez es 0,28 mm y con cada nuevo doblez se duplica. Es decir, se trata de una progresión geométrica en la que a un dobles le corresponde 0,28 mm y la razón r=2. Por tanto el término general de esta sucesión es:
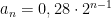
 siendo n el número de dobleces y an el grosor del papel en milímetros.

¿Puedes agarrar la calculadora y comprobar esto?

Con 26 dobleces ya superas la altura del Everest (8.848 metros)

Con 50 dobleces superarás la distancia de la Tierra al Sol (150 millones de kilómetros)

Aquiles y la tortuga
Es posible que hayas oído hablar de esta paradoja, una de las más clásicas y famosas. La describía así el filósofo griego Zenón de Elea en el siglo V a.C.
“Aquiles, el atleta más veloz, corre a alcanzar a una tortuga que huye de él. Cuando llega donde estaba la tortuga, ésta ya ha avanzado un trecho. Cuando Aquiles recorre ese tramo, la tortuga avanza otro poco. Y así sucesivamente, cuando Aquiles llega a donde estaba la tortuga, ésta ya ha avanzado algo. Por tanto, nunca la alcanza.”
Por supuesto, sabes que alcanzará a la tortuga. Pero, ¿cómo puedes desmontar el argumento de Zenón, que asegura que la tortuga siempre lleva alguna ventaja?


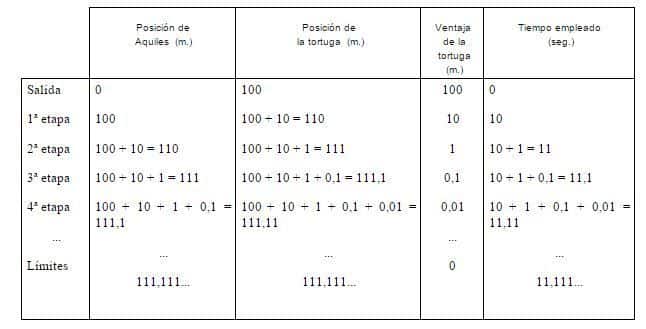
Esta es una forma: La tortuga tiene una ventaja de 100 metros. Imagina que Aquiles (lo conocerás por su talón) es capaz de correr los 100m en 10 segundos, y la tortuga es 10 veces más lenta que él.
Es decir,cuando Aquiles ha cubierto esos 100m, la tortuga se ha desplazado 10m. Al cubrir Aquiles esos 10 m, la tortuga se ha desplazado 1m, Mientras cubre ese metro que le separa de la tortuga, ésta ha recorrido 0’1 m. Y así indefinidamente.
Parece una tontería, pero se tardaron 24 siglos en desvelar por completo esta paradoja, gracias a la Teoría de Límites. La suposición de que infinitos trayectos deben sumar una distancia infinita y necesitan un tiempo infinito no es correcta.

 

En la tabla de arriba puedes ver que Aquiles, según las condiciones iniciales, tardará 11,111... segundos en alcanzar a la tortuga.

Se trata de una progresión geométrica de razón 1/10. La suma de todos los infinitos tiempos es:
 
Acabas de ver que aunque la suma tenga infinitos sumandos, el resultado puede ser finito. Lo mismo que dividir 100 entre 9.